Le langage Pascal

On peut regrouper un ensemble d'instructions sous un même nom. On forme alors un sous-programme ou procédure. On utilise les procédures :

• Chaque fois qu'une même suite d'instructions doit être répétée plusieurs fois dans un programme;
• Quand une suite d'instructions forme une action globale. Le programme est alors plus clair et les erreurs plus facilement détectables.

Pour pouvoir utiliser une procédure, il faut d'abord la déclarer. La déclaration des procédures et fonctions se fait après toutes les autres déclarations.

Structure d'une entité de programme (routine)▲

PROGRAM remplir (output);
   {entête du prog principal}

VAR i : integer;
   {déclarations prog princ.} 

   {dont déclaration LIGNE}
PROCEDURE ligne(n:integer);
   {entête de la procédure} 
var j : integer;
   {déclarations procédure}
BEGIN
  {corps de la procédure}
  for j := 1 to n do write('*');
  writeln 
END;

BEGIN
  {instructions du prog princ}
  for i := 1 to 25 do ligne(70)
END.

Celle-ci est symbolisée dans l'exemple ci-dessus par deux cadres : la variable I et la procédure LIGNE (avec un argument entier) sont déclarées dans REMPLIR, et donc connues dans tout le programme (rectangle extérieur). Par contre N et J sont déclarés dans LIGNE et ne sont connus (et utilisables) que dans le rectangle intérieur.

En d'autres termes :

• Une variable est locale pour une procédure X si elle est déclarée dans X. Elle n'existe que dans X (et dans les procédures déclarées à l'intérieur de X). La routine qui comporte la procédure X ne peut donc pas accéder à cette variable locale.
• Une variable est globale pour une procédure X si elle est déclarée dans une routine englobant la procédure X. Elle peut être utilisée dans la procédure. La modifier la modifie également dans la routine appelante (englobante).

Si l'on avait déclaré une variable I dans la procédure LIGNE (au lieu de N ou J), celle-ci aurait été locale à la procédure, c'est à dire que, dans le programme principal, I désigne une autre case mémoire que dans la procédure. Modifier la variable localeI ne modifie pas la variable globaleI (momentanément inaccessible).

Remarque : Ceci s'applique à toutes les déclarations. En particulier, une procédure déclarée localement à l'intérieur d'une procédure est indéfinie à l'extérieur.

Les échanges d'informations entre une routine et une sous-routine peuvent se faire par l'intermédiaire des variables globales. Mais il est beaucoup plus intéressant d'utiliser les paramètres : (6)

PROGRAM machin (input,output);

VAR
  a, b, c, d : real;

PROCEDURE aff_somme(x,y:real);
var z : real;
begin
  z := x + y;
  writeln(x ,' + ', y ,' = ', z)
end;

BEGIN {	programme principal }
  writeln('Entrez 4 valeurs :');
  readln(a,b,c,d); 
  aff_somme(a,b); 
  aff_somme(3,5); 
  aff_somme(c+a,d) 
END.

En appelant AFF_SOMME(A,B), la procédure prend pour x la valeur de a, et pour y la valeur de b. On dit que les arguments sont passés par valeur. Mais si la procédure modifiait x ou y, a et b ne seraient pas modifiés dans le programme appelant. Pour répercuter les modifications des arguments, il faut les déclarer comme variables (ils sont alors dits passés par adresse).

PROCEDURE echange (VAR x, y : real); 
var z : real; 
begin 
  z := x; 
  x := y; 
  y := z 
end; {cette procédure échange les contenus des 2 arguments}

Tout ce qui a été dit pour les procédures s'applique également aux fonctions. La différence avec une procédure est qu'une fonction renvoie un résultat.

L'entête est du type :

FUNCTION nom_fonction (liste_parametres) : type_de_la_fonction

La liste des paramètres (en général passés par valeur) est de la même forme que pour une procédure, le type de la fonction étant le type du résultat retourné. On retourne le résultat par :

NOM_FONCTION := ...

Exemple :

PROGRAM classer (input,output); 

VAR a, b, c : real; 

FUNCTION max (x, y : real) : real; 
begin 
  if x >= y then 
    max := x 
  else max := y 
end; 

BEGIN
  writeln('Entrez deux valeurs : '); 
  readln(a,b); 
  c := max(a,b); 
  writeln('Le plus grand est ',c) 
END.

La fonction max a deux paramètres réels (x et y) et renvoie un réel.

C'est ainsi que l'on appelle le fait qu'une routine puisse s'appeler elle-même.

function factorielle (n : integer) : integer; 
begin 
  if n <= 1 then 
    factorielle := 1 
  else 
    factorielle := n * factorielle(n - 1) 
end;

Par exemple, en appelant factorielle(3), on calcule 3 * factorielle(2). Or, factorielle(2) = 2 * factorielle(1), qui lui vaut 1. Donc factorielle(3) = 3 * (2 * 1) (ce qui me parait juste). Faites un petit dessin, à chaque appel on recrée de nouvelles variables locales, donc on obtient 3 cases n distinctes valant 3, 2 et 1, on les supprime petit à petit en passant sur le END.

Remarque : Il faut toujours vérifier qu'en aucun cas on ne puisse avoir une boucle infinie qui bloquerait la machine. Ce serait le cas en mettant le test IF N = 1 et en appelant factorielle pour une valeur négative ou nulle.

Une procédure devant toujours être déclarée pour pouvoir être utilisée, on utilise FORWARD pour les cas de récursivité passant par deux procédures :

function prem (a, b : real) : boolean; FORWARD; { déclaration anticipée de l'entête }

procedure deux (x, y : real);
var vbool : boolean;
begin
  ......
  vbool := prem(x,y); { on peut utiliser PREM car déjà déclarée }
  ......
end;

function prem; { ne plus donner les arguments car déjà déclarés }
begin
  ......
  if pas_fini then
     deux(a,b); { DEUX déjà déclarée }
  ......
end;

Exercicerec :
Ecrire le programme qui calcule le déterminant d'une matrice carrée NxN sachant que celui-ci vaut :

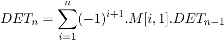
où M[i,1] est l'élément de la matrice (ligne i, 1ère colonne),
DETn-1 est le déterminant de la sous-matrice d'ordre n-1 obtenu en ôtant la ligne i et la 1ère colonne.
Le déterminant d'une matrice 1x1 est son seul élément.
On utilisera bien évidement une fonction récursive, et l'on séparera le calcul de sous-matrice dans une procédure.
Remarque : Il existe des méthodes numériques permettant d'accéder au résultat beaucoup plus rapidement que par cette méthode.
Voir la correction